Volume Formula For Hexagonal Prism
Expanse and Volume of Hexagonal Prism
Given a Base of operations edge and Height of the Hexagonal prism, the job is to observe the Surface Expanse and the Volume of hexagonal Prism. In mathematics, a hexagonal prism is a three-dimensional solid shape which accept 8 faces, eighteen edges, and 12 vertices. The two faces at either ends are hexagons, and the rest of the faces of the hexagonal prism are rectangular.

where a is the base length and h is the height of the hexagonal prism.
Surface Area =
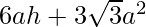
Volume =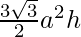
Examples:
Input : a = 4, h = 3 Output : Surface Area: 155.138443 Volume: 124.707657 Input : a = 5, h = ten Output : Surface area: 429.904 Volume: 649.519
C++
#include <bits/stdc++.h>
using namespace std;
void findSurfaceArea( float a, float h)
{
bladder Expanse;
Expanse = 6 * a * h + 3 * sqrt (3) * a * a;
cout << "Surface Expanse: " << Surface area;
cout << "\n" ;
}
void findVolume( float a, bladder h)
{
bladder Volume;
Book = 3 * sqrt (three) * a * a * h / 2;
cout << "Volume: " << Volume;
}
int main()
{
float a = 5, h = 10;
findSurfaceArea(a, h);
findVolume(a, h);
return 0;
}
Coffee
import java.io.*;
class GFG {
static void findSurfaceArea( bladder a, float h)
{
bladder Area;
Area = 6 * a * h + 3 * ( float )(Math.sqrt( 3 )) * a * a;
System.out.println( "Surface Area: " + Surface area);
}
static void findVolume( float a, float h)
{
bladder Volume;
Volume = 3 * ( float )(Math.sqrt( 3 )) * a * a * h / ii ;
Organization.out.println( "Volume: " + Volume);
}
public static void main (String[] args)
{
float a = 5 , h = x ;
findSurfaceArea(a, h);
findVolume(a, h);
}
}
Python3
import math
def findSurfaceArea(a, h):
Surface area = 0 ;
Area = ( 6 * a * h +
three * math.sqrt( three ) * a * a);
print ( "Surface Surface area:" ,
circular (Area, 3 ));
def findVolume(a, h):
Volume = 0 ;
Volume = ( 3 * math.sqrt( 3 ) *
a * a * h / 2 );
impress ( "Book:" ,
circular (Volume, 3 ));
a = 5 ;
h = 10 ;
findSurfaceArea(a, h);
findVolume(a, h);
C#
using System;
class GFG
{
static void findSurfaceArea( float a,
bladder h)
{
float Area;
Area = 6 * a * h + 3 *
( float )(Math.Sqrt(iii)) * a * a;
Console.WriteLine( "Surface Area: " +
Area);
}
static void findVolume( float a,
float h)
{
float Volume;
Book = iii * ( float )(Math.Sqrt(3)) *
a * a * h / 2;
Console.WriteLine( "Volume: " +
Volume);
}
public static void Main ()
{
float a = 5, h = 10;
findSurfaceArea(a, h);
findVolume(a, h);
}
}
PHP
<?php
part findSurfaceArea( $a , $h )
{
$Expanse ;
$Surface area = half-dozen * $a * $h + iii *
sqrt(three) * $a * $a ;
repeat "Surface Area: " ,
$Surface area , "\n" ;
}
function findVolume( $a , $h )
{
$Volume ;
$Volume = three * sqrt(3) *
$a * $a * $h / two;
echo "Volume: " , $Volume ;
}
$a = 5; $h = ten;
findSurfaceArea( $a , $h );
findVolume( $a , $h );
?>
Javascript
<script>
office findSurfaceArea( a, h)
{
let Area;
Area = 6 * a * h + 3 * Math.sqrt(3) * a * a;
document.write( "Surface Area: " + Surface area.toFixed(three) + "<br/>" );
}
function findVolume( a, h)
{
permit Volume;
Volume = 3 * Math.sqrt(3) * a * a * h / 2;
document.write( "Volume: " + Volume.toFixed(3));
}
let a = 5, h = x;
findSurfaceArea(a, h);
findVolume(a, h);
</script>
Time complexity : O(1) as performing constant operations
Auxiliary Space : O(1)
Volume Formula For Hexagonal Prism,
Source: https://www.geeksforgeeks.org/surface-area-and-volume-of-hexagonal-prism/
Posted by: daviswillith1981.blogspot.com


0 Response to "Volume Formula For Hexagonal Prism"
Post a Comment